POLYEDRES de CATALAN
On les appelle ainsi car c’est E. Catalan qui les découvrit en
cherchant des polyèdres semi-
réguliers.
Définition : On appelle polyèdre de catalan
celui dont les faces sont égales et dont les angles polyèdres
sont réguliers. (E. Catalan )
Les faces n’ont pas ici à être inscrites dans un cercle,
elles ne sont donc pas nécessairement des polygones réguliers.
Propriétés :
-
Ce sont les duaux des polyèdres
archimédiens.
-
Leurs duaux sont les polyèdres
archimédiens.
-
Ils sont inscriptibles et circonscriptibles à une sphère.
-
Ils sont au nombre de
quinze :
Tétraèdre à toits, dodécaèdre rhombique,
octaèdre à toits, cube à toits, Icositétraèdre
deltoïde, dodécaèdre à diamant, icositétraèdre
pentagonal (droit et gauche), triacontaèdre rhombique, icosaèdre
à toits, dodécaèdre à toits, hexacontaèdre
deltoïde, triacontaèdre à diamant, hexacontaèdre
pentagonal (droit et gauche).
|
|
|
|
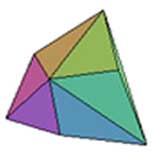
Tétraèdre à toits
|
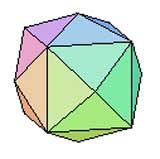
Cube à toits
|
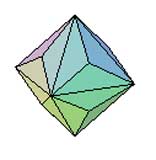
Octaèdre à toits
|
|
|
|
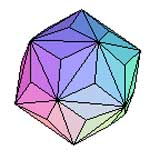
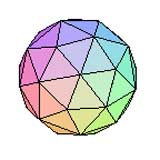
Icosaèdre à toits
|
Dodécaèdre à toits
|
|
|
|
|
|
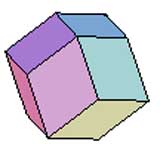
Dodécaèdre Rhombique
|
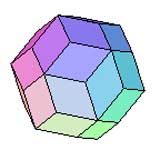
Triacontaèdre Rhombique
|
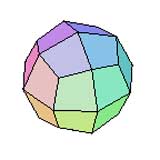
Icositétraèdre Deltoïde
|
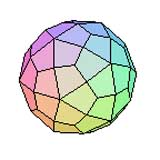
Hexacontaèdre deltoïde
|
|
|
|
|
|
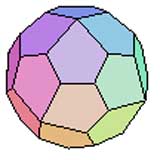
Icositétraèdre Pentagonal
|
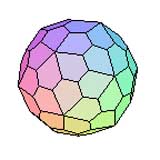
Hexacontaèdre Pentagonal
|
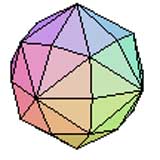
Dodécaèdre à diamants
|
Triacontaèdre à diamants
|
polyèdres
de platoniciens
polyèdres de Kepler-Poinsot
polyèdres archimédiens
polyèdres de Johnson
polyèdres uniformes
retour à la page d'accueil...
dernière mise à jour le 29 Mai
2000