 |
 |
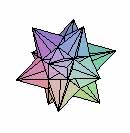
| Petit dodécaèdre étoilé | Grand dodécaèdre étoilé |
 |
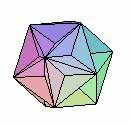 |
| Grand Icoasèdre | Grand Dodécaèdre |
Ils sont aussi connus sous le nom de solides de Kepler-Poinsot, Kepler ayant découvert les deux premiers, Poinsot les deux autres.
Définition : un polyèdre régulier concave
(ou étoilé)
est un polyèdre dont toutes les faces sont égales à
un même polygone régulier, complet ou étoilé,
et dont tous les angles diédres (c’est à dire les angles
entre deux faces possédant une arrête commune) sont égaux.
Propriétés :
 |
 |
| Petit dodécaèdre étoilé | Grand dodécaèdre étoilé |
 |
 |
| Grand Icoasèdre | Grand Dodécaèdre |
|
|
|
|
|
|