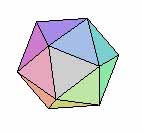
Ils sont aussi connus sous le nom de polyèdres platoniciens car ils ont été décrit par Platon dans le Timée.
 

Définition : un polyèdre régulier convexe est un polyèdre inscriptible dans une sphère et dont toutes les faces sont des polygones réguliers convexes isométriques (c’est à dire que toutes les arêtes auront même longueur).
 

Propriétés :

1. Toutes les faces du polyèdre sont superposables.
2. Tous les angles diédraux (c’est à dire les angles entre deux faces possédant une arrête commune) sont égaux.
3. Tous les sommets sont formés par le même nombre de faces.
4. Comme on peut le montrer à l’aide de la formule d’Euler, il n’existe que 5 polyèdres réguliers convexes : le tétraèdre, le cube (ou hexaèdre), l’octaèdre, le dodécaèdre et l’icosaèdre.

Tétraèdre
Cube	Octaèdre
Dodécaèdre	Icosaèdre

Si on lève la restriction sur la convexité, on obtient les quatre polyèdres réguliers concaves, dit de Kepler-Poinsot.

Si on lève la restriction sur le fait que les polyèdres doivent être superposables, on obtient des polyèdres semi- réguliers convexes : les polyèdres Archimédiens.