On leur donne aussi le nom de solides archimédiens.

Définition : On appelle polyèdre archimédien celui dont les faces sont des polygones réguliers et dont les angles polyèdres sont égaux (ou symétriques). (E. Catalan)

NB : les polyèdres réguliers convexes répondent aussi à cette définition, mais ils ne sont pas reprit.

Propriétés :

1. Toutes les arêtes ont même longueur.
2. Ils sont inscriptibles et circonscrits à une sphère.
3. Ils ont les mêmes groupes d’isométrie que les polyèdres platoniciens.
4. Leurs duaux sont les polyèdres de Catalan.
5. On peut montrer, à partir de la formule d'Euler, qu'ils sont au nombre de quinze.

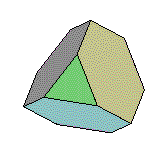
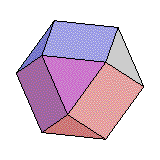
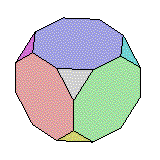
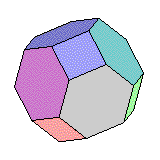
Tétraèdre Tronqué	Cuboctaèdre	Cube Tronqué	Octaèdre Tronqué
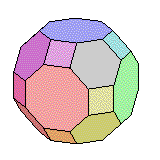
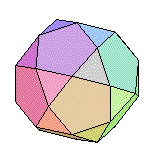
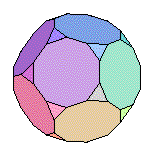
Petit Rhombicuboctaèdre	Grand Rhombicuboctaèdre	Icosidodécaèdre	Dodecaèdre Tronqué
Icosaèdre Tronqué	Petit Rhombicosidodécaèdre		Grand Rhombicosidodécaèdre
Snub Cube		Snub Dodécaèdre

---

         polyèdres de platoniciens             polyèdres de Kepler-Poinsot                       polyèdres de Catalan                   polyèdres de Johnson                       polyèdres uniformes

---

retour à la page d'accueil...

---

dernière  mise  à jour le 29 Mai 2000


---