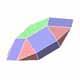
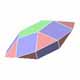
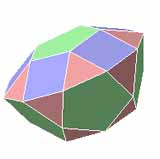
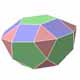
Les polyèdres de Johnson sont des polyèdres convexes ayant des faces régulières (à l'exception des solides platoniciens qui sont totalement réguliers, des solides archimédiens qui sont semi- réguliers et des deux familles de prismes et antiprismes).

Il existe 28 polyèdres de Johnson simples, c'est à dire pouvant être coupés par un point plan en deux polyèdres aux faces régulières, en plus des prismes et antiprismes.

Johnson proposa (1966) et Zalgaller prouva (en 1969) qu'il existait en tout exactement 92 polyèdres de Johnson.

Nous donnons ci-dessous la liste des polyèdres de Johnson: