DERIVES
     
    1. Polyèdres duaux : deux polyèdres sont duaux (ou conjugués) s'ils sont l'un inscrit et l'autre circonscrit à une même sphère, de façon que les sommets du premier soient les pôles des faces du second, et vice versa, deux arêtes correspondantes quelconques sont réciproques. 
    Le dual du dual d'un polyèdre considéré est ce même polyèdre. 

    Pour construire le dual d'un polyèdre donné, on considère les milieux des faces de ce polyèdre. Ces milieux sont des points qui forment l'ensemble des sommets du polyèdre dual (inscrit).

     
    		2. Snub : procédé chiral qui remplace chaque arête par une paire de triangles. Par exemple, le snub cube, dérivant du cube, est construit de manière suivante : les 6 faces carrées du cube restent des carrés mais légèrement tournés, les 12 arêtes deviennent 24 triangles et les 8 sommets deviennent 8 triangles de plus. Il est à noter que si l'on applique ce même processus à l'octaèdre (dual du cube), on obtient le même résultat à savoir six faces carrés entourées de 20 faces triangulaires. On nomme donc parfois le snub cube et le snub octaèdre d'un nom commun : snub cuboctaèdre. 

    Il en est de même pour le snub dodécaèdre et le snub icosaèdre appelés tous deux snub icosidodécaèdre. 

     
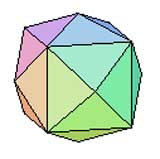    		3. -Kis : processus d'addition de nouveaux sommets au centre de chaque face afin de les utiliser pour diviser chaque n-faces en triangles. 

    Plus concrètement, on prend les centres des faces et on tire dessus pour obtenir des pyramides. Par exemple, le cube tétrakis, encore appelé cube à toits, est obtenu à partir du cube auquel on a ajouté des pyramides à base carrée (d'où le tétra-kis) sur chaque face. De même pour le dodécaèdre pentakis (ou dodécaèdre à toits).

     
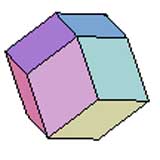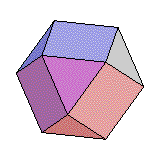
    		4. Rhombique : Ce mot signifie losange (voir dans Nomenclature). On peut construire un polyèdre rhombique à partir d'un cube, octaèdre ou d'un dodécaèdre, icosaèdre. Il faut pour cela en faire des kis et en faisant varier la hauteur des pyramides on obtient des faces coplanaires deux à deux qui froment des losanges. Par exemple le dodécaèdre rhombique.

     
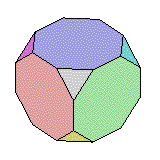
    5. Troncature : processus consistant à couper les coins du polyèdre. Comparons par exemple le cube et le cube tronqué : la troncature ajoute de nouvelles faces à chaque coin du cube, et remplace les six faces carrées par des faces octogonales. Plus généralement, les n-faces (faces à n côtés) sont replacées par des 2n-faces (faces à 2n côtés) 
    Si on coupe les coins jusqu'au milieu des arêtes du polyèdre, les nouvelles faces sont régulières, en partant du cube, on obtient le octaèdre.

     
    		6. Etoilé : processus d'extension des faces du polyèdre. En fait, on prolonge les faces pour en obtenir de nouvelles. Il y a plusieurs manières de le faire, donnant des résultats différents. Par exemple, le petit dodécaèdre étoilé et le grand dodécaèdre étoilé (qui sont des polyèdres de Kepler-Poinsot).

     
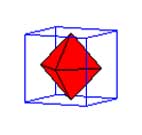
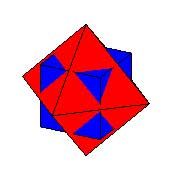
    image de la Stella Octangula 7. Composés : processus d'interpénétration de plusieurs polyèdres, identiques ou connexes. On obtient alors souvent une figure assez esthétique, plus ou moins régulière. Exemple : La Stella Octangula de Kepler est un composé de deux octaèdre et d'un cube inscrits l'un dans l'autre.

     

    retour en haut de la page ...                                                      retour à la page d'accueil ...
    dernière mise à jour le 27 Mai 2000