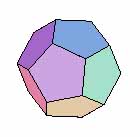
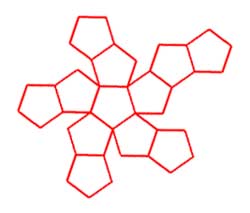
Ledodécaèdre est un polyèdre régulier convexe. Il a :
 

nombre de sommets S =	20
nombre de faces F =	12	On a donc la vérification de la formule d'Euler : S + F - A = (20+12-30) = 2
nombre d'arêtes A =	30

Le groupe de symétrie du dodécaèdre est le groupe de l'icosaèdre.
Le dual du dodécaèdre est l'icosaèdre.